80%ループ機だと平均5連
90%ループ機だと平均10連など
なんとなく知っている人は多いと思いますが、
数学的にどのように計算するのか気になる人もいると思うので、
パチンコの平均継続数(連荘数)の求め方を簡単ですがまとめてみました。
今回はわかりやすく
確変突入率80%、確変継続率80%というシンプルな台を想定して
計算方法を学びます。
考え方
考え方は簡単で、連荘回数の期待値を求めます。
単発終了確率×1
+
2連する確率×2
+
3連する確率×3
+
:
+
n連する確率×n
+
2連する確率×2
+
3連する確率×3
+
:
+
n連する確率×n
上記のように
連荘確率と連荘数の和が平均連荘数となります。
計算方法
確変突入率が80%、確変継続率が80%なので、
上記を数式にすると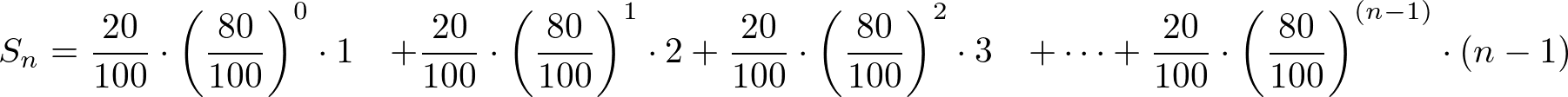
上記の式となります。
この数式は
(等比)×(等差)数列の和です。
等比×等差数列の和は
Snへ公比を掛けてずらした数式を元の数式から引いて等比数列の和へ変換して計算します。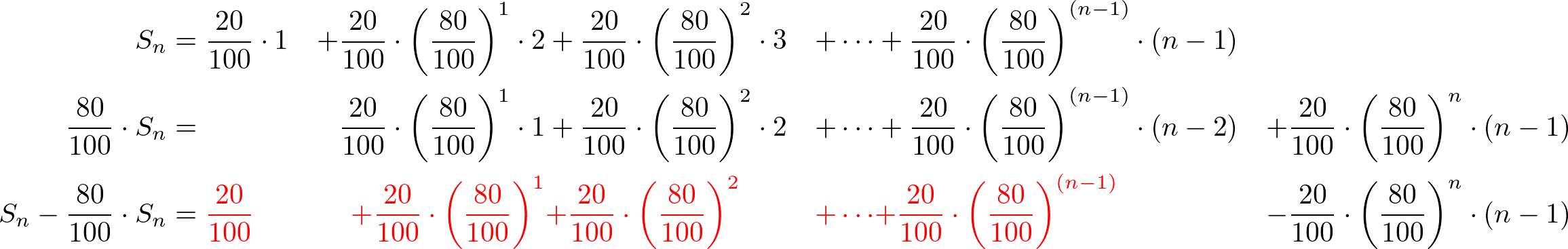
つまり上記画像のようになります。
赤字部分は
公比が-1<r<1の無限等比級数が収束するので、
下記の公式を利用します。
赤字部分で初項は100分の20、公比は100分の80となるので、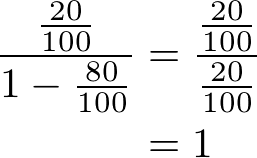
そして、Snの極限を取ります。
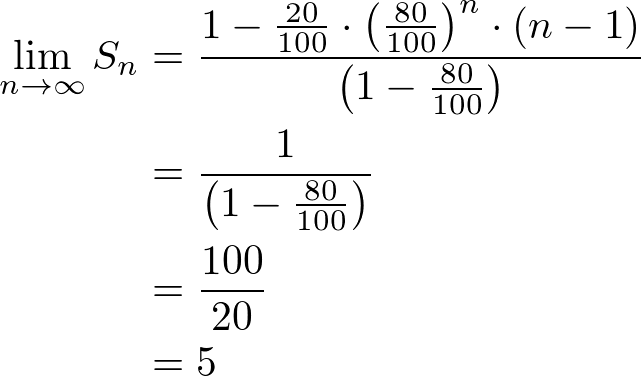
-1から1までの数字のn乗の極限は0となるので
数式内のnが消えて
結果5となりました。
よって
確変突入率が80%、確変継続率が80%の平均連荘数は5連となります。
公式
いろいろと遠回りをしましたが、
最後の数式をみてもらうと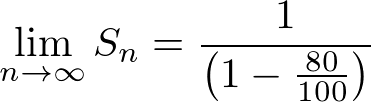
となってます。
つまり継続率は
というとっても簡単な式で求めることができます。
継続率が90%であれば
100÷(100-90) = 10 なので 10連荘
継続率が70%であれば
100÷(100-70) = 3.3333… なので 3.33連荘
といった感じで簡単に計算することができます。
パチンコを打つ人は覚えておいて損はない公式ですね。

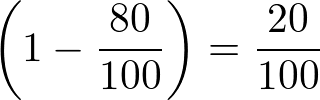
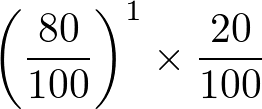
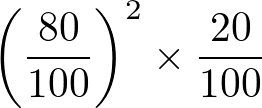
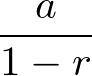
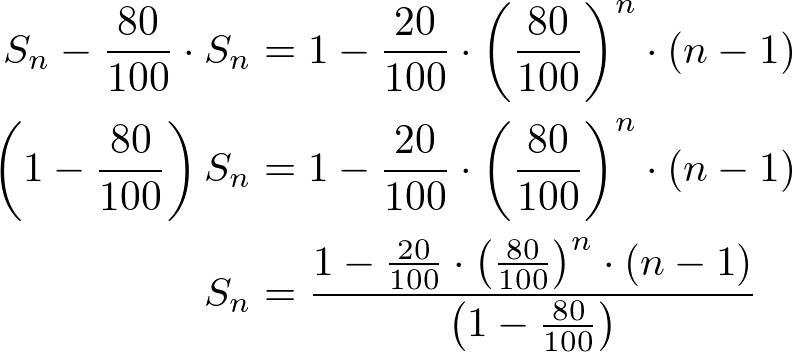
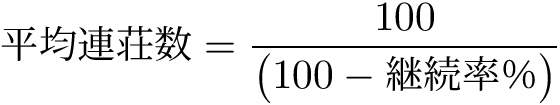




コメント