Aタイプ1000円50枚で
何回転回すことができるのかの計算の仕方を簡単に解説したいと思います。
現在でも絶賛稼働中の
プレミアムハナハナ-30の小役確率を元に解説します。
プレミアムハナハナ-30の小役確率
※下記は設定1の小役確率となります。
| 確率 | 払出 | |
|---|---|---|
| ベル | 7.7 | 8枚 |
| リプレイ | 7.3 | 3枚(リプレイ) |
| チェリー | 48 | 2枚 |
| スイカ | 160 | 10枚 |
基本的な考え方
1000円50枚で回る回転数を求める際は
1回転当たりの期待値を求めて計算します。
例えばベルを引いた場合
3枚投入し、払い出しが8枚なので
7.7分の1で+5枚の期待値となります。
これを全小役分足した数字が1回転当たりの期待枚数。
50枚÷(1回転当たりの期待枚数)=1000円の回転数
となります。
ハズレ確率を求める
すべての小役確率+ハズレ確率が1となるので、
1=ベル確率+リプレイ確率+チェリー確率+スイカ確率+ハズレ確率
移行すると
ハズレ確率 = 1-(ベル確率+リプレイ確率+チェリー確率+スイカ確率)
となります。
当てはめると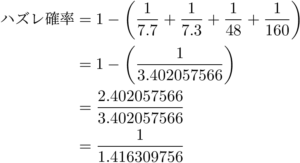
よってハズレ確率は1.42分の1となります。
1回転当たりの期待値
ハズレ確率が求められましたので、
小役確率を元に1回転当たりの期待値を求めると
| 確率 | 払出 | 払出ー投入 | 期待値 | |
|---|---|---|---|---|
| ベル | 7.7 | 8枚 | +5枚 | +0.65 |
| リプレイ | 7.3 | 3枚 | 0枚 | 0.00 |
| チェリー | 48 | 2枚 | -1枚 | -0.02 |
| スイカ | 160 | 10枚 | +7枚 | +0.04 |
| ハズレ | 1.42 | 0枚 | -3枚 | -2.12 |
上記のようになります。
期待値をすべて足すと
-1.45枚。
つまり1回転で1.45枚ずつ減っていきます。
1000円50枚当たりの回転数
1回転当たり1.45枚ずつ減っていきますので、
50枚÷1.45枚が回転数となります。![]()
つまり1000円50枚で約34.6回転回すことができます。
※小役確率が小数点第1位までで省略されてますので、大分ずれが出ます。




コメント
ベルの期待値0.65の差出式がわかりません。
できれば教えてくれませんか?